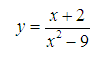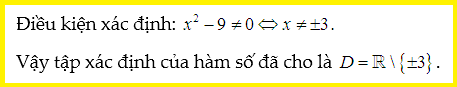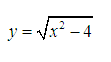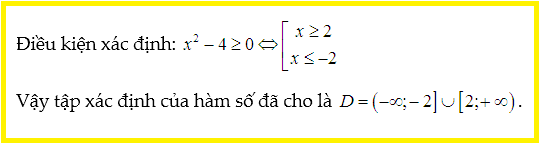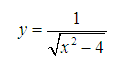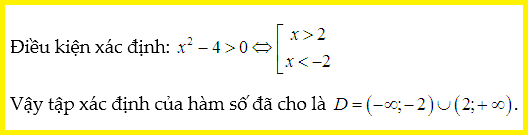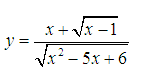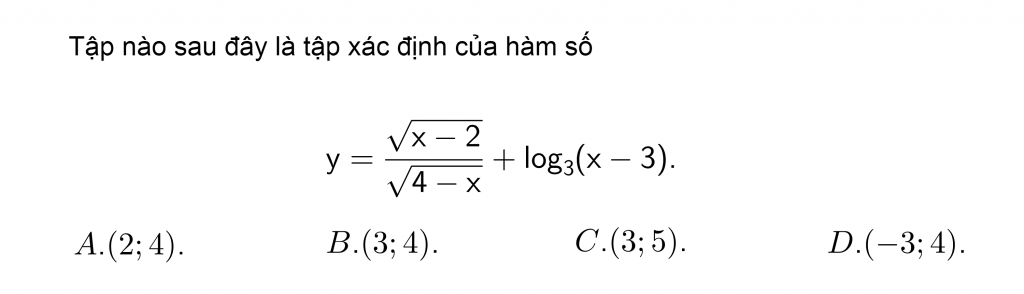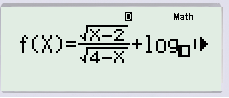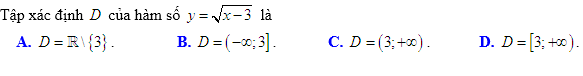Tìm tập xác định của hàm số ở lớp 10
Tìm tập xác định của hàm số là dạng toán quan trọng. Bởi vì trong nhiều bài toán về hàm số mà chúng ta không xét tập xác định của hàm số đó có thể dẫn đến việc giải sai. Trong bài viết này sẽ hướng dẫn các em cách tìm tập xác định trong phạm vi lớp 10 và cách sử dụng Casio để giải nhanh. Chúng ta cùng bắt đầu nhé.
Content
TẬP XÁC ĐỊNH CỦA HÀM SỐ LÀ GÌ
Tập xác định của hàm số y=f(x) là tập con của R bao gồm các giá trị sao cho biểu thức f(x) xác định.
Ví dụ:
Số 3 không thuộc tập xác định của hàm số y=1/(x-3) vì khi ta thay số 3 vào biểu thức 1/(x-3) thì không tính được. Số 5 thuộc tập xác định vì khi thay số 5 vào ta tính được kết quả là 1/2. Rõ ràng đối với hàm số này chúng ta thấy có rất nhiều giá trị khác thuộc tập xác định. Chẳng hạn như: 1; 2; 4…
Vì vậy tìm tập xác định của hàm tức là tìm tất cả các giá trị của biến mà khi thay vào biểu thức của hàm ta tính được.
TÌM TẬP XÁC ĐỊNH CỦA HÀM SỐ TOÁN 10
Đối với chương trình toán 10 thì các hàm cần tìm tập xác định có biểu thức đơn giản hơn các lớp sau. Các công thức xác định hàm số mới chỉ bao gồm các loại như chứa căn và chứa mẫu. Vì vậy tùy vào công thức của hàm số chúng ta chia ra làm các loại như sau cho dễ làm (Chú ý là ở lớp 10 nhé, lớp sau sẽ khác đấy):
Loại 1: Hàm không chứa căn và không chứa mẫu thì tập xác định là R. Ví dụ như hàm số bậc nhất y=ax+b và hàm số bậc 2 y=ax²+bx+c (a≠0) là các hàm có tập xác định là R.
Loại 2: Hàm số chứa ẩn dưới mẫu thì mẫu cần khác 0.
Ví dụ:
Tìm tập xác định của hàm sau:
Lời giải:
Loại 3: Hàm số chứa ẩn trong căn bậc chẵn thì trong căn phải lớn hơn hoặc bằng 0 (Căn không dưới mẫu) hoặc trong căn lớn hơn hẳn 0 (Căn dưới mẫu).
Ví dụ:
Tìm tập xác định của hàm sau:
Lời giải:
Nhận xét: Đây là trường hợp căn không dưới mẫu.
Ví dụ:
Tìm tập xác định của hàm sau:
Lời giải:
Nhận xét: Đây là trường hợp căn dưới mẫu. Tác giả chọn biểu thức gần với ví dụ trên để các em học sinh tiện so sánh.
Chú ý: Trong một hàm mà có chứa nhiều loại như đã nêu ở trên. Bởi vì chúng ta cần tất cả các điều kiện phải xác định nên ta cần viết tất cả các điều kiện và phải đặt trong dấu hệ.
Ví dụ:
Tìm tập xác định của hàm sau:
Lời giải:
CÁCH TÌM TẬP XÁC ĐỊNH CỦA HÀM SỐ BẰNG CASIO
Phương pháp dùng MTBT này khá hữu ích trong các toán trắc nghiệm mà phương án của nó rõ ràng. Ý tưởng dùng casio xuất phát từ việc khai thác chức năng CALC hoặc TABLE. Chúng ta cùng theo dõi một ví dụ đề hiểu hơn nhé.
Ví dụ:
Lời giải:
Ở đây mình dùng dòng máy Vinacal 570 ES Plus II. Các dòng máy khác sử dụng hoàn toàn tương tự.
Trước tiên ta vào chức năng MODE 7 để nhập hàm số đã cho.
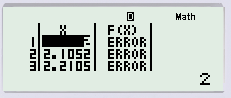
Để kiểm tra phương án A ta chọn START bằng 2, END bằng 4 và STEP bằng (4−2)/19.
Ta thấy trên khoảng (2;4) xuất hiện các giá trị bị ERRO. Vậy ta loại phương án A. Cứ như vậy cho đến khi còn phương án B. Chọn B.
Mỗi phương pháp đều có ưu điểm và nhược điểm riêng. Vì vậy tùy vào đề bài cụ thể các em hãy lự chọn phương pháp phù hợp cho mỗi dạng toán nhé.
BÀI TẬP VỀ TẬP XÁC ĐỊNH HÀM SỐ LỚP 10
Click câu hỏi để xem đáp án.
Câu 1:
Câu 2:
Nhận xét: (Nhận xét này mang tính chủ quan)Tìm tập xác định của hàm số lớp 10 phần nào đó sẽ đơn giản hơn ở các lớp sau. Bởi vì mỗi lớp chúng ta lại học thêm 1 vài hàm số nữa sẽ tăng lượng kiến thức lên. Chẳng hạn như lớp 11 chúng ta học thêm hàm số lượng giác, lớp 12 chúng ta học thêm hàm số lũy thừa, mũ, logarit. Mỗi loại hàm lại có cách tìm tập xác định khác. Các em cùng xem bài viết dưới đây để tìm hiểu thêm nhé.
Chúc các em thành công!
Xem thêm
Hàm số bậc nhất bậc 2 -