Phương pháp chứng minh hai mặt phẳng vuông góc
Dạng toán chứng minh hai mặt phẳng vuông góc là một dạng toán quan trọng trong hình học không gian. Bài viết này sẽ hướng dẫn các bạn cách giải dạng toán này.
1. GÓC GIỮA HAI MẶT PHẲNG
Trước hết, các bạn cần hiểu khái niệm góc của hai mặt phẳng. Theo định nghĩa gốc sách giáo khoa thì góc giữa 2 mặt phẳng là góc giữa 2 đường thẳng lần lượt vuông với 2 mặt phẳng đó.
Tuy nhiên định nghĩa sau đây sẽ trực quan và dễ sử dụng hơn.
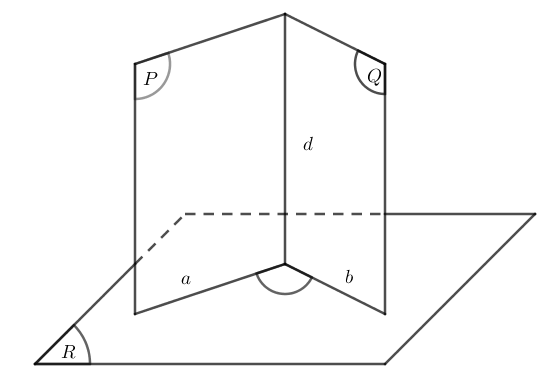
Giả sử có hai mặt phẳng (P) và (Q) cắt nhau theo giao tuyến d. Mặt phẳng (R) vuông góc với đường thẳng d cắt (P) và (Q) theo giao tuyến a và b. Khi đó góc giữa đường thẳng a và b chính là góc giữa (P) và (Q).
Trường hợp hai mặt phẳng song song hoặc trùng nhau thì góc của chúng bằng 0°.
Mặt phẳng (P) vuông góc với mặt phẳng (Q) nếu góc của chúng bằng 90°.
Hình ảnh bức tường và nền nhà cho chúng ta hình dung về hai mặt vuông góc với nhau.
2. CÁCH CHỨNG MINH HAI MẶT PHẲNG VUÔNG GÓC
Nói chung thì xác định góc giữa 2 mặt phẳng cũng không đơn giản. Nên ta thường dùng cách khác để chứng minh 2 mặt phẳng vuông góc với nhau.Trước hết ta cần nắm được tính chất hai mặt phẳng vuông góc như sau:
- Tính chất 1: Nếu 2 mặt phẳng vuông góc với nhau thì đường thẳng nào nằm trong mặt phẳng này vuông góc với giao tuyến thì cũng vuông góc với mặt phẳng kia và ngược lại.
- Tính chất 2: Nếu trên mặt phẳng này có chứa một đường thẳng vuông góc với mặt phẳng kia thì 2 mặt phẳng đó vuông góc với nhau.
Chú ý: Tính chất 1 thường được dùng để chứng minh đường vuông góc với mặt. Tính chất 2 được dùng để chứng minh 2 mặt phẳng vuông góc. Cụ thể là ta quy bài toán chứng minh 2 mặt phẳng vuông góc thành bài toán chứng minh đường vuông góc với mặt. Còn để chứng minh đường thẳng vuông góc với mặt phẳng thì ta chứng minh đường thẳng đó vuông góc với 2 đường thẳng cắt nhau nằm trong mặt phẳng.
Để hiểu rõ hơn các bạn hãy theo dõi ví dụ sau:
Ví dụ:
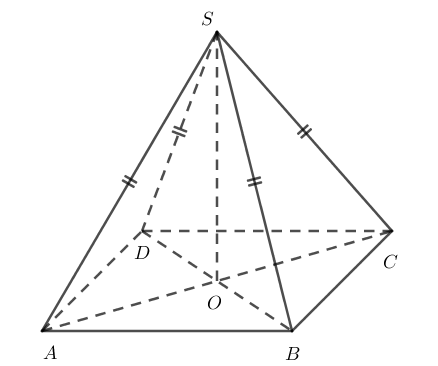
Cho hình chóp S.ABCD có ABCD là hình vuông và SA=SB=SC=SD. Chứng minh rằng (SAC)⊥(ABCD).
Giải:
Phân tích: Ta phải tìm một đường nằm trong đáy vuông với (SAC). Hoặc tìm một đường nằm trong (SAC) vuông với đáy.
Vì giả thiết có các cạnh bên SA=SB=SC=SD nên ta chọn phương án thứ 2.
Gọi O là tâm của đáy.
Vì các tam giác SAC và SBD là các tam giác cân nên SO vuông với các đường AC và BD.
Do đó SO vuông góc với (ABCD).
Mà SO nằm trên mặt phẳng (SAC). Do đó (SAC)⊥(ABCD).
Trên đây là lý thuyết và hướng dẫn chứng minh hai mặt phẳng vuông góc trong không gian. Thuộc kiến thức hình học lớp 11. chúc các bạn học tập vui vẻ!
Vectơ - Quan hệ vuông góc -